如下图,多边形的六个角分别代表六种三角函数,存在如下关系:
1)对角相加乘积为1,即sinθ·cscθ=1;cosθ·secθ=1;tanθ·cotθ=1。
2)多边形任意相邻的三个顶点代表的三角函数,处于中间位置的函数值等于与它相邻两个函数值的乘积,如:sinθ=cosθ·tanθ;tanθ=sinθ·secθ...
3)阴影部份的三
六个三角函数也可以根据直径为1中心为原点的单位圆来定义。单位圆定义在实际估算上没有大的价值;实际上对多数角它都依赖于直角三角形。并且单位圆定义的确容许三角函数对所有负数和正数辐角都有定义,而不只是对于在0和π/2弧度之间的角。它也提供了一个图象,把所有重要的三角函数都包含了。按照勾股定律,
三角函数
单位圆的多项式是:对于圆上的任意点(x,y),x²+y²=1。
图象中给出了用弧度测度的一些常见的角:逆秒针方向的测度是正角,而顺秒针的测度是负角。设一个过原点的线,同x轴正半部份得到一个角θ,并与单位圆相交。这个交点的x和y座标分别等于cosθ和sinθ。图象中的三角形确保了这个公式;直径等于底边且宽度为1,所以有sinθ=y/1和cosθ=x/1。单位圆可以被视为是通过改变邻边和对边的宽度,但保持底边等于1的一种查看无限个三角形的形式。
对于小于2π或大于等于2π的角度,可直接继续绕单位圆旋转。在这些方法下,余弦和正弦弄成了周期为2π的周期函数:对于任何角度θ和任何整数k。
周期函数的最小正周期称作这个函数的“基本周期”。余弦、余弦、正割或余割的基本周期是全圆,也就是2π弧度或360°;余弦或余切的基本周期是半圆,也就是π弧度或180°。里面只有余弦和正弦是直接使用单位圆定义的,其他四个三角函数的定义如图所示。
在余弦函数的图象中,在角kπ附近变化平缓,而在接近角(k+1/2)π的时侯变化迅速。余弦函数的图象在θ=(k+1/2)π有垂直渐近线。这是由于在θ从右侧接进(k+1/2)π的时侯函数接近正无穷,而从两侧接近(k+1/2)π的时侯函数接近负无穷。
三角函数
另一方面,所有基本三角函数都可根据中心为O的单位圆来定义,类似于历史上使用的几何定义。非常是,对于这个圆的弦AB,这儿的θ是对向角的一半,sinθ是AC(半弦),这是美国的阿耶波多介入的定义。cosθ是水平距离OC,versinθ=1-cosθ是CD。tanθ是通过A的切线的线段AE的厚度,所以这个函数才叫余弦。cotθ是另一个切线段AF。secθ=OE和cscθ=OF是割线(与圆相交于两点)的线段,所以可以看作OA顺着A的切线分别向水平和垂直轴的投影。DE是exsecθ=secθ-1(正割在圆外的部份)。通过这种构造,容易看出正割和余弦函数在θ接近π/2的时侯发散,而余割和余切在θ接近零的时侯发散。
根据单位圆定义,可以做三个有向线段(向量)来表示余弦、余弦、正切的值。如图所示,圆O是一个单位圆,P是α的终边与单位圆上的交点,M点是P在x轴的投影,A(1,0)是圆O与x轴正半轴的交点,过A点做过圆O的切线。
这么向量MP对应的就是α的余弦值,向量OM对应的就是正弦值。OP的延长线(或反向延长线)与过A点的切线的交点为T,则向量AT对应的就是余弦值。向量的起止点不能颠倒,由于其方向是有意义的。
角形,处于上方两个顶点的平方之和等于下顶点的平方值,如:
;
;
。
变化规律
余弦值在
随角度减小(降低)而减小(降低),在
随角度减小(降低)而降低(减小);
正弦值在
随角度减小(降低)而减小(降低),在
随角度减小(降低)而降低(减小);
余弦值在
随角度减小(降低)而减小(降低);
余切值在
随角度减小(降低)而降低(减小)。
注:以上其他情况可类推,参考第五项:几何性质。
不仅上述六个常见的函数,还有一些不常见的三角函数:
乎乎的小手上,他摇动着身子,小手在黑白键上随便联通,脚趾在地上一起一落,谁都不晓得他在弹些哪些。他虽然很迷醉似的紧锁眼睛,微抿小嘴,吟唱着一些毫不搭调的乐曲,满身的欢喜。
他是我的儿子,一个对音乐一窍不通的小女孩,时常坐到我的琴前,就会表现出一副音乐家的姿态,在琴键上恣意激扬他对于音乐的热爱。
曾几何时,我也像他一样,秉持着一份热情,投入一项爱好,难以自拔。我会在一张画纸上,滚落小小的情绪,虽然画工非常肤浅;我会在动听的曲目里,不由自主地歌唱,虽然嗓音不这么嘹亮;我会用单反,用心记录下沿途所见的景色,虽然技术并不精良……我想,人生在世,不必在乎这些细枝末节,学会在平静如水的生活中,用右手扬起朵朵浪花,找寻生活的情趣,捉住已逝的时光里的每一个小缝隙。会玩,才好。喜欢约上三两个好友,登上高高的山顶,在天宇下放声歌唱。在山顶上歌唱,耳朵是空空的,心是明朗的。当自己的歌声从那方的山传回时,心是飘飘的,飘出了躯壳,飘到了天上,与浮云做伴,与天宇相栖。唱到满天繁星,唱到街灯通明,唱
春暖花正开,我们都是一群开始学会浅忆的儿子,总是喜欢自由的穿梭在季节的半度微凉里,行走着,也不断找寻着,那种温暖季节里不老的青春,那种夏天中哭过笑过的日子。
凉凉的风迅速躲进每位刚出课室的人的肩膀里,吸干所有温暖然后扬长而去。一个个班级排着不太整齐的队型围着操场跳着,踩着还恋恋不舍离去的风,循环似地跑。在这个沙土满天飞的地方,这个用多少泪水浇灌过仍然没有变样的地方,这个满天飞舞着梦想羽毛的地方。我,我们都在进行着一场不容许暂停的旅程。
卸下了厚实的围巾、手套,每位人都变得清新多了,这或许就是夏天对我最大的馈赠吧。迫不及待换上纤弱衣物的我也任时光在我孱弱的青春里放肆地穿行,这个季节也记载着我们“时光不老,我们不散”的誓言。在高中仅存的七十多天里,开始享受着泪水沾湿外套的畅快,开始挥笔将一件件旧事定格在朋友录上,虽然这种奢华的纸掩藏不住每位人内心的伤。那些都是这个季节的附送品,我像是个提早拆开了包装的人,没理由拒绝。其实,还不是最悲伤的五月,但我早已开始练习释怀,预演着一颗不会哭泣的心。事实证明是我无能,放不下这珍稀的七年时光,走不出这个温暖到伤悲的夏天。
2019年的秋天,我们说好一起走下去,就当作我两年高中生活的最终结局,就当我们关于这个季节的约定。
阳光将浓雾暖开了,化作一滩水花落在地上,无声无息中视界清晰了,空气中参杂着这个季节原本的甜美。远山轮廓分明,中学里新栽的玉兰花吐蕊待放,一切都在期盼着。备考、订正习题成了每晚的生活,和每位高中中学生一样,习惯性地在练习本上零乱地写着运算步骤,将算出的答案无比认真的写在试题上,用显眼红笔圈改着,看着练习册上那未曾相熟的题目。时常抬头凝望几下我眼里总有云飘过的天空。这个夏天,我们仍然在成长,如同铭刻着生命中一段独一无二的岁月。
每天都是打在过道里的几米阳光,老师们总不时地向我们脑中灌输着“努力学习,再拼上两个月”的信息。在这样的日子里,看个电视剧成为了每位中学生最大的奢华。看书、复习成了我仍然坐在桌子前的动力。假如说春天是每位结业生都抱成一团哭的季节,这么夏天就是每位结业生奋斗努力的季节。所以,阳光正明媚,路上花正开,我们正行走着。
纵容心飞行,原先夏天始终都在,不想把季节的更迭囚禁在月历上。我想那应当是一种无休止的奔跑。蓝天白云绿草地,任由心情行走在自然的芬芳里,我憧憬着,这淡然的岁月,这时常会渴望着的秋冬时节。我想夏天就是这样一种意境吧,像天空中的云一样,自己飘出一个世界,无论生活给与的是感伤还是快乐,这静谧的春始终都在。忙碌之中,仍有季节陪我走。
到耐不住山风的
三角函数是基本初等函数之一,是以角度(物理上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点座标或其比值为因变量的函数。也可以等价地用与单位圆有关的各类线段的厚度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础物理工具。在物理剖析中,三角函数也被定义为无穷级数或特定微分等式的解,容许它们的取值扩充到任意实数值,甚至是复数值。
常见的三角函数包括余弦函数、余弦函数和余弦函数。在航海学、测绘学、工程学等其他学科中,都会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。不同的三角函数之间的关系可以通过几何直观或则估算得出,称为三角恒方程。
三角函数通常用于估算三角形中未知宽度的边和未知的角度,在导航、工程学以及数学学方面都有广泛的用途。另外,以三角函数为模版,可以定义一类相像的函数,称作双曲函数。常见的双曲函数也被称为双曲余弦函数、双曲正切函数等等。三角函数(也称作圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。三角函数一般定义为包含这个角的直角三角形的两个边的百分比,也可以等价的定义为单位圆上的各类线段的厚度。更现代的定义把它们抒发为无穷级数或特定微分等式的解,容许它们扩充到任意负数和正数值,甚至是复数值。
严冬时,我们才舍得离去。
喜欢背上钢琴,去到远方的原野,与轻风流水应和。弹自己最爱的乐曲,想自己最怀念的同学:她在那儿还好吗,她是否过得快乐呢?喜欢周杰伦的《枫》中的“缓缓飞舞的枫叶像想念,我燃起烛光温暖年末的春天”,但是我的想念如同那绵绵不断的轻风,像那缓缓而过的流水。我多想用自己仅会的几首乐曲,来温暖自己心灵的夏天。
喜欢到小城的小吃街上,去找寻不一样的辣味。油泼辣子淌在软糯修长的拉面上“滋滋”作响,一清二白三红四绿的寿司也别具辣味。当晶莹透亮的面条弹入唇瓣时,激爽的炎夏又多了一分风韵。尝的是油盐酱醋茶,品的是生活的甜酸苦辣咸。喜欢在晚霞的余晖里,捧上一本最爱的书,缅怀又三天的已逝。谢谢东坡先生教会我,要始终保持“仰天大笑出门去”的豁达旷达;谢谢青莲居士教会我,要在平静无奇的生活中找寻甜蜜;谢谢易安居士教会我,要在逆境学校会抗争……还喜欢《简·爱》中女主人公的人格独立,喜欢《红楼梦》中林哥哥的“腹有诗书气自华”,喜欢《追风筝的人》中哈桑的虔敬善良……
这种催泪的书,这种不平凡的人物,伴我走过美好的青葱时光。谢谢,感恩。
会玩,才好。在生活中会玩,在玩学校会生活。在忙碌的生活学校会自我宣泄,用一颗向下的心去感知生活的美好,才才能活得舒服,活得有意义。这么,玩上去假如才能把疾患也全数剿灭,这么这份苦难又将由(例如说)像貌丑恶的人去承当了。即使我们连丑恶,连愚蠢和无耻和一切我们所不喜欢的事物和行为,也都可以统统剿灭掉,所有的人都一样健康,漂亮,聪敏,高尚,结果会如何呢?怕是人间的折子戏就全要收场了,一个丧失差异的世界将是一条死水,是一块没有觉得没有肥力的荒漠。
4、浩倡。《九歌·东皇太一》:“陈竽瑟兮浩倡”。“浩倡”又作“浩唱”,和上句“安歌”相对应。起名时可改为“浩昌”。下文《九歌·少司命》中还有“浩歌”。令诸校屯寿春梅领待命。
▼
中国有句俗语,叫“林子大了,哪些鸟都有”。
这回,我算是再度领教了……
穿胸罩就受孕了,这可能吗?
近来,网上见到这样一则新闻:
#我母亲穿大家家内衣受孕了#
事情的缘由是一位女客户在某家店面买了条短裤。
结果过了段时间,她便气魄汹汹地找上客服,直接来了一句话:
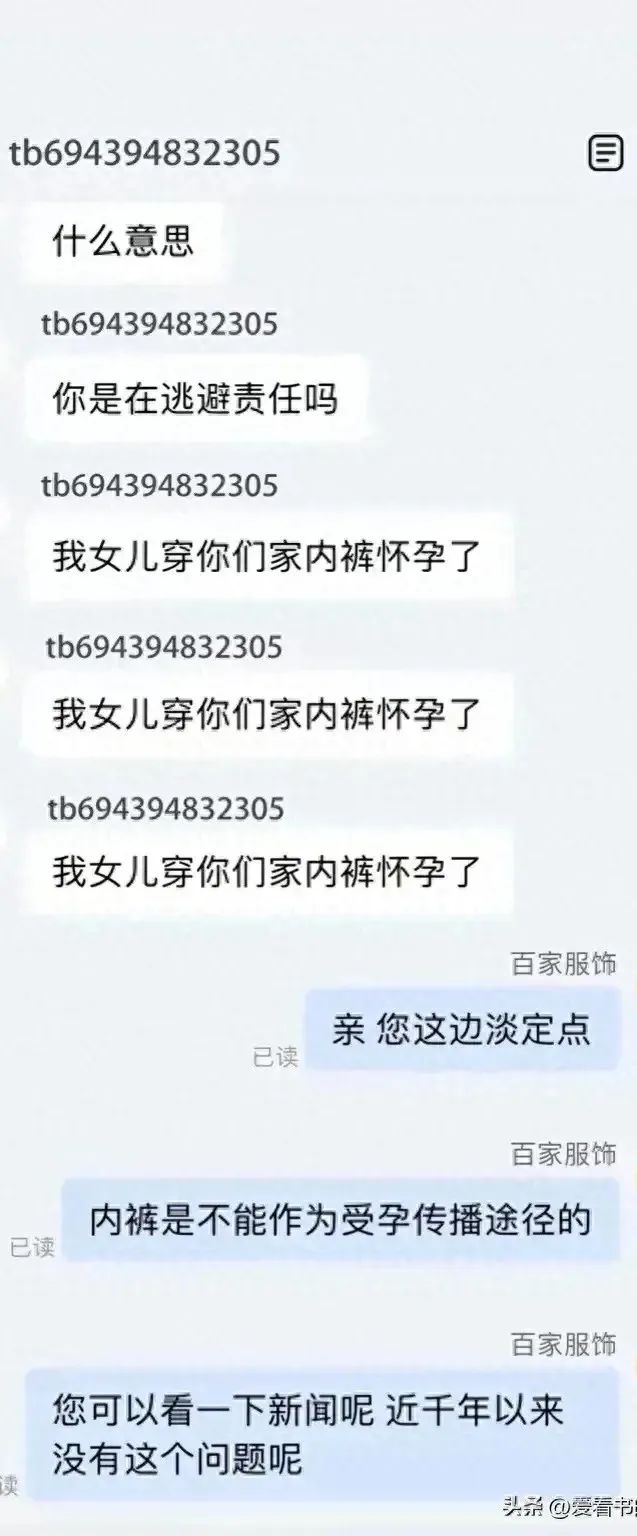
“我母亲穿你家内衣受孕了!”
这话一出,客服小妹妹直接懵圈了。
但她还是尽量保持专业,耐心解释:亲,您那边淡定点,胸罩是不能作为怀孕传播途径的。
本以为如此一说,客户能明白过来,结果对方尚且不领情,还更带劲了:
“什么意思,你这是在逃避责任吗?等着投诉吧大家!”
孕期的事儿能怪到一条裤子身上?
这么违反科学常理的事,真不晓得那位女客户是如何说出口的。
虽然明眼人都能看得下来,她的目的就是想“白嫖”。
客服小妹妹也是被逼急了,直接使出杀手锏。
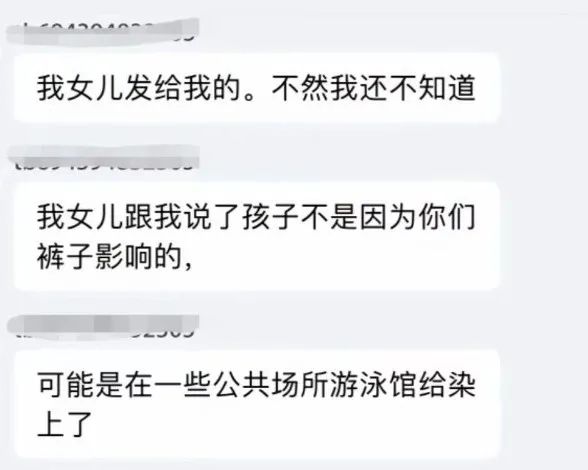
她解释说,咱家鞋厂里,不仅老总是男的,其他全是女职工,但是老总早就结扎了,您说这如何可能嘛?
这一招,直接把话题从内衣受孕的雷人事儿转移到了老总的丑事上。

全网围观下,除了老总的态度“崩”了,就连女客户自己也顶不住压力,下来澄清了。
这一澄清,游泳馆又无辜躺枪,成了新的“背锅侠”。
你说这事儿,是不是很离谱?
见过雷人的,没见过如此雷人的。
由于此事太过离奇,也有人指责这是段子,为噱头侵吞流量,不是真实例子。
姑且不论这个段子真伪,现实里这事儿还真不稀少,说的就是这些“白嫖党”。

有些人
吃相真的太难看了
买东西收钱是天经地义的事情。
不满意也可以退货退款,这更是我们的权力。
可自从“七天无理由退款”、“仅退票”等机制出现,我才晓得自己低估了人性。
去年末,去南京游览的旅客中,有部份人穿着带吊牌的鹅绒服下来了。

为何不摘下吊牌?7天无理由退款呗。
游览扫兴返家,鹅绒服食不上了,就退掉。
甚至就连穿得脏兮兮的雪地靴都退了。
这早已不是白嫖了,这叫厚颜卑劣,与市井无赖无异。
前段时间,“仅退货动了谁的芝士”该话题更是冲热搜,网友揶揄称之为“0元购”。
许多店家堪称是苦不堪言。
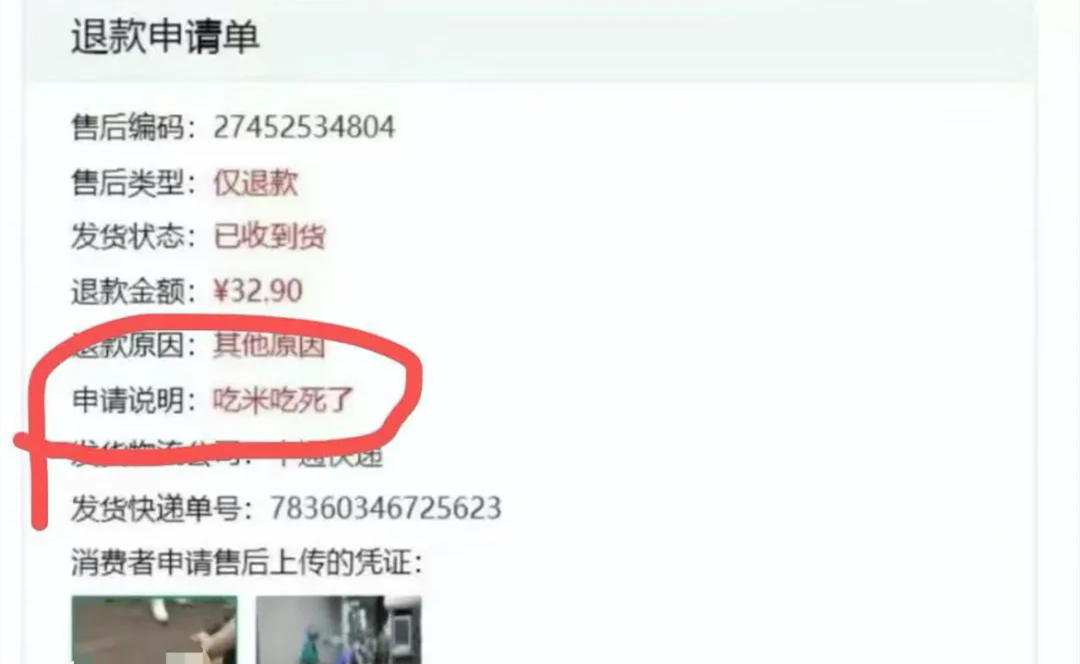
在仅退票“原因说明”那一栏,你可以听到下边这种雷人理由。
“没钱了。”

“吃米吃死了。”
可以说,只有我们想不到的,没有白嫖党撒不了的谎。
最最可悲的是哪些?是那些人除了自己白嫖,还出教程教人怎样实现“白嫖”。
真是无话可说了。
为何这么多人喜欢白嫖?
说白了,就是贪排尿宜。
贪排尿宜的人
早晚会要不得
人都有贪排尿宜的心理。
顺手牵羊,不要白不要,占人实惠……
但有句话是如此说的:贪排尿宜要不得,不图实惠不上当。
前几天我在网上滑水,见到一个挺火的视频,视频的主角是一位女学院生。
这女孩把自己裹得跟个蒙面高手似的,就露俩耳朵,在寝室里念致歉信。
这信是给谁的呢?是给某个电商店家的。
为何谢罪?由于她干了件不太地道的事儿——白嫖。
事情是这样的,她从网上一家店买了东西,东西一到手,心思就活络了,想来个“空手套白狼”,直接申请仅退货。
更绝的是,她还编了个谎话,说是店家自己发错货了,想把锅甩给人家。
沟通过程中,说话还不客气,挺冲的。
但此次,她算是踢到铁板了。
店家没惯着她,直接找上门来,让她录谢罪视频发社交平台。

你说她贪那点排尿宜图个啥?
最后不光面子丢了个干净,也彻底曝露了自己的修养和品性,真是得不偿失。
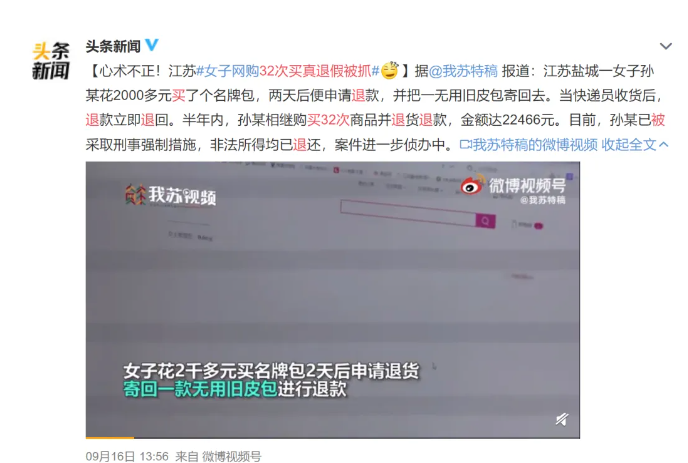
还有河南淮北一个女生孙某,她发觉了网购平台的一个“小技巧”——极速退票服务。
这服务挺便捷的,快件员一上门把东西拿走,不等店家验货,钱就嘶嘶地退回去了。
于是,孙某半年时间里,前后买了32次衣物、鞋子、包包啥的,收到货后呢,把新买的宝贝留下,把家里一堆废旧物品打包好,直接退给了店家。
但好景不长,这世上哪有不漏风的墙。
店家们也不是吃肉的,察觉到了不对劲,赶快报了警。
孙某自以为很聪明,到头来却吃上了官司。
爱占实惠的人,终究是占不了实惠。
拾得眼前一芥草,错失身旁万木春。
《菜根谭》中说:“不求非分之福,不贪无故之获。”
不贪大便宜,才是一个人最大的精明。

一旦规则倒塌
掩埋的将是每一个人
其实有人会指责:薅羊绒是每位消费者的权力,有些实惠就该占。
“难道只能让平台获利,不能让消费者获利。”
虽然,“白嫖党”、“羊毛党”不仅仅是占大便宜这么简单。
主持人董卿有句话说得十分好:炸雷之下,没有赢家。
一人作恶,一群人遭难。
规则一旦被滥用,无人才能幸免。
还记得麦当劳曾推出的32元自助沙拉吗?
规则简单,一人一次机会,装多少全看你的能耐。
沙拉台上,都是些家常菜品,茄子、玉米、黄瓜、苹果,价钱稍为低点的是草莓罐头。
可就那么点东西,愣是把人潮给引爆了,沙拉区天天跟赶集似的,人挤人。
网上那阵子可热闹了,关于这自助沙拉的功略满天飞——“如何吃垮麦当劳”、“如何将沙拉塔叠到最高”……
网友们一个个变身建筑师,把沙拉叠成高高的“沙拉塔”,吃不完就打包回去。

最后,麦当劳实在是抵挡不住,只能把沙拉吧给撤了。
虽然,再大的店家也经不起如此疯狂的“薅羊绒”啊!
你看,贪排尿宜的人一旦被“疯狂”喂养,那我们这种守规则的人的利益才会被损害,最终你们都不好过。
断送社会风气的,也正是这种喜欢贪排尿宜的人。
所以,生而为人,请勿必保有底线。
不做损人利己之事。
不要忘了将心比心。
但愿我们每位人都能自我约束,革除小聪明,涵养大智慧。
与所有人自勉。
往期推荐
版权声明
本文仅代表作者观点,不代表百度立场。
内容来源于互联网,信息真伪需自行辨别。如有侵权请联系删除。












发表评论